Jeg er netop startet op med et B→A-hold og vi starter op med de trigonometriske funktioner. For at få styr på radianer tænkte jeg, at de skulle lave enhedscirkel-stafetten, som jeg tidligere har skrevet om.
Men jeg indså (heldigvis allerede under planlægningen), at det ville være for svært for eleverne at finde ud af, hvor fx 5π/4 er placeret, så jeg måtte finde på en opvarmnings-opgave.
Derfor lavede jeg et opgaveark med to opgaver:
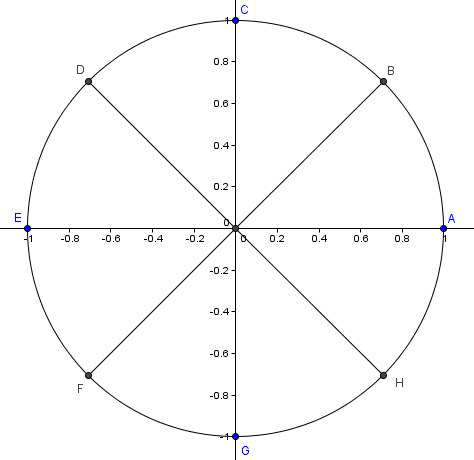
- Enhedscirklen deles i otte lige store stykker og eleverne skal nu finde vinkel og radian for de otte retningspunkter.
- Enhedscirklen deles i 12 lige store stykker og eleverne skal nu finde vinkel og radian for de 12 retningspunkter.
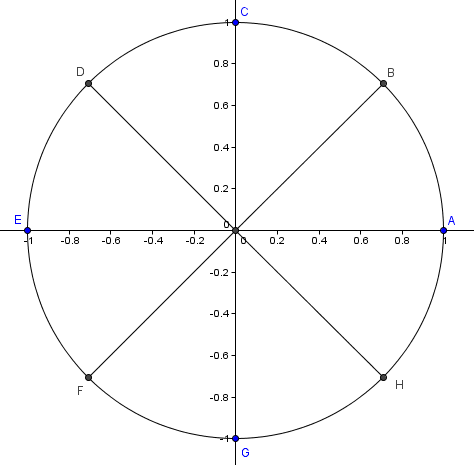
Meningen er her, at de får fornemmelsen af, at man tæller hhv. fjerde- og sjettedele. Altså 1/4, 2/4, 3/4, 4/4, 5/4, 6/4, 7/4 og 8/4 (tilføj selv et π alle steder). Og de skal bemærke at nogle af disse brøker kan forkortes.
Derfor fandt jeg på en “opvarmning til opvarmnings-opgave”: Jeg lavede små kort med alle brøkerne, som de bruger i opvarmningsopgaven – både de uægte og de ægte brøker (fx både 2π/4 og π/2) og så skal eleverne samle de kort, der er lig med hinanden. Nogle kort ligger alene, mens der fx er tre kort der er lig π.
Samlet set blev programmet altså
- Hvilke brøker er lige store? (link til kort)
- Opgaver med enhedscirklen (lav en meget kort tavlegennemgang inden)
- Enhedscirkel-stafet (link til kort)
- Med kort inden for intervallet [0;2π]
- Negativ omløbsretning forklares og der dystes nu med kort inden for intervallet [-2π;2π]
- Flere omløb forklares og der dystes nu med kort inden for intervallet [-∞;∞]
Det tog ikke et helt modul (vores er 95 minutter), så vi havde tid til overs til at se nærmere på de trigonometriske funktioner.

Comments