Det der med at holde alle elever i gang i timen kan godt være udfordrende. Men her er en ide, der kan skabe aktivering -. og læring! Jeg beskriver metoden med et konkret eksempel, men du kan til sidst i indlægget se forslag til andre emner, hvor metoden kan bruges.

Hvem er hvem?

Vi er i gang med differentialregning (2g B-niveau), og eleverne skal have styr på graferne for f og f’. Derfor har jeg lavet en lang række billeder af to grafer, der er hhv. f og f’. Eleverne skal så afgøre, hvem der er hvem. På billederne er graferne rød og blå, og derfor udstyres hver elev med to pap-kort – et rødt og et blåt.

Først viste vi på tavlen en række grafer (f og f’) og eleverne skulle så svare ved at vise den farve seddel, som de mente var grafen for f’. Når de havde svaret var det let at vælge en elev og spørge til argumentet for elevens valg.

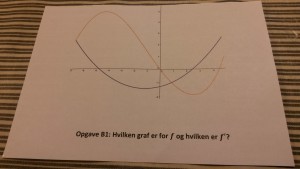
Derefter lagde jeg en række opgaver ud på bordene i skolens fællesmområde. Eleverne skulle så i små grupper gå rundt til opgaverne og skrive ned hvilken af graferne der var f’. Opgaverne var nummererede og eleverne fik hver et svarark til at notere deres svar.

Derefter gennemgik vi opgaverne ved tavlen (det behøver man ikke gøre med alle opgaverne), og her skulle man så svare på de af opgaverne, som man havde nået at lave i grupperne. Også her er det en god ide at kræve et argument fra en af de elever, der svarer. Også gerne en, der har svaret forkert.

Trold:

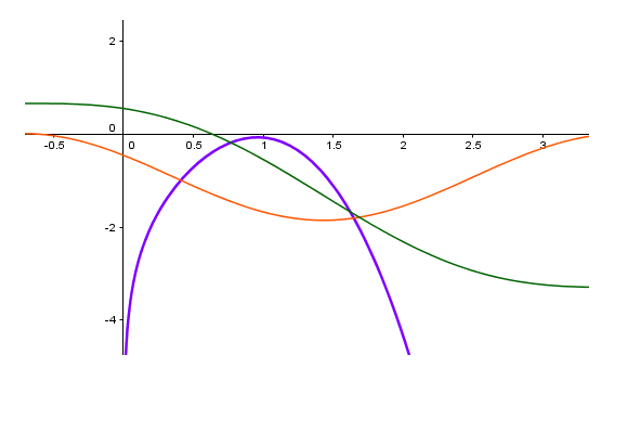
Jeg opdagede, at eleverne (for) let fandt ud af hvad der var f og f’ så derfor lavede jeg en version med en “trold” – altså en tredje funktion. Så kommer der en ekstra farve i spil, og eleverne skal derfor have et ekstra farve-kort.

Praktisk:

• Kortene til eleverne er karton i A7-format (altså et A4-ark, der er delt i 8). Jeg har som oftest en bunke med forskellige farver liggende i tasken.
• Funktionerne har jeg lavet i et GeoGebra-dokument (uden trold – med trold), der genererer forskellige funktioner (forskellige typer med forskellige konstanter). Graferne for en af funktionerne og dens afledte vises med to/tre forskellige farver. Jeg har så taget skærmklip af graferne og indsat i et Word-dokument, så formatet var printvenligt.

 

Andre muligheder

Jeg forestiller mig, at man kan bruge kort-metoden til mange andre emner – bl.a. dem jeg har beskrevet i mit indlæg om slå først-quizzen. Hvor quizzen har fokus på spil og konkurrence bliver metoden med kort mere med fokus på argumenter.

• Voksende/aftagende: Eleverne får igen to kort, som repræsenterer hhv. svaret voksende og aftagende. Eleverne kan så svare for en række funktionsforskrifter (fx, lineær, eksponentiel, potens eller en blanding). Man kan bruge mit GeoGebra–ark med tilfældigt genererede funktioner (lineær, eksponentiel, potens).
• Funktionstype: Man kan som i EPL-quizzen spørge efter hvilken væksttype, der er tale om (lineær, eksponentiel, potens). Du kan finde GeoGebra-arket med quizzen her
• 0, 1 eller “noget andet”: Jes Sixtus har på son blog lavet en 0, 1 eller “noget andet”-quiz, hvor man også kan bruge kort til at repræsentere de tre svarmuligheder. Du kan læse om Jes’ quiz og se hans quiz-dokument her.
• Andengradspolynomier: Fortegn for a, c og d . Tilfældige andengradspolynomier kan genereres i dette GeoGebra-dokument.
• Differentiere omvendt: Som introduktion til integralregningen beder jeg eleverne differentiere omvendt. Jeg viser dem altså f’ og de skal så gætte hvad f er. Svaret beder jeg dem skrive på et stykke papir og holde det op så jeg kan se deres svar. For ikke at spilde en masse papir tager jeg en stak fejlprint i kopirummet. Og så har jeg givet eleverne som lektie, at de skal medbringe en tusch (så jeg tydeligt kan se deres svar). Du kan læse mit indlæg om At differentiere omvendt her.

 

Hvad synes du om indlægget?